9
L'hypothèse des trous noirs
Préambule
En 1784, devant l'auditoire de la Royal Society de Cambridge, le révérend John Michell, géologue et astronome amateur anglais suggéra “que les particules de lumières étaient attirées de la même façon que les autres corps”. A partir de cette hypothèse fondamentale, il formula pour la première fois le concept de trou noir : ”si disait-il, le demi grand-axe d’une sphère de même densité que le Soleil dépassait le rayon de celui-ci dans une proportion de 1 à 500, alors un corps, tombant d’une hauteur infinie vers lui, aurait acquis à sa surface une plus grande vitesse que celle de la lumière, et par conséquent, en supposant que la lumière soit attirée par la même force en proportion de sa force d’inertie, comme d’autres corps, toute la lumière émise par un tel corps y retournerait, par sa propre gravité”. Il expliquait que malgré le fait que ces corps étaient invisibles, ils devaient provoquer des effets gravitationnels décelables : “s’il arrivait que quelque autre corps lumineux tourne autour d’eux, des mouvements de ces corps tournants, nous pourrions peut-être encore déduire l’existence du corps central avec quelque degré de probabilité; cela pourrait aussi bien nous apporter une indication concernant quelques unes des irrégularités des corps tournants, qui ne serait pas aisément explicable par aucune autre hypothèse”. Mais la thèse de Michell restait trop abstraite et ne recevra aucun écho. Il faudra attendre 1796 pour que le marquis Pierre Simon de Laplace, mathématicien, philosophe et astronome passionné par la mécanique céleste et la gravitation redécouvre cette idée. Il écrivait dans son Exposition du Système du Monde : "Un astre lumineux, de la même densité que la Terre, et dont le diamètre serait 250 fois plus grand que le Soleil, ne permettrait, en vertu de son attraction, à aucun de ses rayons de parvenir jusqu'à nous. Il est dès lors possible que les plus grands corps lumineux de l'univers puissent, par cette cause, être invisibles". Il présentera sa thèse devant l'auditoire de l'Académie des Sciences mais ceux-ci resteront sceptiques sur les chances d'existence d'un tel objet. Ainsi naquit le concept du trou noir mais la démonstration mathématique de Laplace semblait fantaisiste aux yeux des astronomes.
Robert Oppenheimer et Hartland Snyder démontrèrent l'existence des singularités en 1939, concluant : "Quand toutes les sources d'énergies thermonucléaires seront épuisées, une étoile suffisamment massive s'effondrera", c'est le trou noir de Schwarzschild.
C'est finalement le physicien John Wheeler de l'Université de Princeton qui, en 1967 dénomma "trou noir" une telle singularité et l'enveloppe qui l'entoure. Les français auraient bien aimé l’appeler “astre occlus” en hommage à Laplace, mais le terme anglais traduit bien le caractère mystérieux qui recouvre cette entité. Elle est à la fois cachée à nos regards au sens strict et a un grand impact d'un point de vue psychologique.
(Extrait de "Le trou noir" par Thierry LOMBRY)
1 

1.1 

La métrique de Schwarzschild extérieure
(9.1.1)
Avec
Présente à
première vue une singularité si .
C'est l'abbé Lemaître qui pensa que cette singularité n'était due qu'au choix
des coordonnées.
|
Exemple
d'un "mauvais" choix de coordonnées : L'équation
de la surface d'une sphère de rayon Comme
En
posant Il
y a apparemment une singularité lorsque Ce
paradoxe disparait avec un nouveau changement de variable :
|
1.2 Changement de variables
Le changement de variables proposé est :
(9.1.2)
En calculant
En choisissant
les fonctions telles que
(9.1.3)
il reste
En choisissant maintenant
(9.1.4)
C'est-à-dire
(9.1.5)
1.3 



Les équations (9.1.3) et (9.1.4) permettent de déterminer
les fonctions .
En élevant la première au carré en en soustrayant la seconde :
Soit
(9.1.6)
Il faut se
rappeler que et donc que
Si
et
En posant on trouve, à une constante additive près :
(9.1.7)
Et d'après (9.1.3) ,
et avec (9.1.6)
(9.1.8)
En intégrant sot
et
(9.1.9)
D'après (9.1.5) .
Et d'après le résultat ci-dessus :
(9.1.10)
La singularité
n'apparait plus que si ,
c'est-à-dire
.
Lorsque
alors
et pour cette valeur de
:
.
La singularité mathématique a disparu.
Dans cette métrique toutes les horloges sont synchronisées !
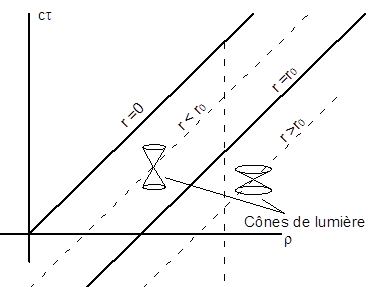
Une particule
immobile dans ce référentiel a une ligne d'univers .
Elle est représentée par une droite "verticale" dans le diagramme
ci-dessus. Pendant un intervalle de temps
fini les particules se précipitent vers le
centre du champ (
) qui est un point de singularité réel de la
métrique.
2 

Pour un rayon
lumineux ,
s'ils sont radiaux
et sans restreindre la généralité on supposera
Et
(9.2.1)
Les signes correspondent aux 2 frontières du cône de
lumière au point d'univers donné.
(9.2.2)
3 

Si ,
la ligne d'univers
de pente 1, se trouve à l'intérieur du cône de
lumière et la particule peut se déplacer dans différentes directions.
Si ,
la ligne d'univers
,
se trouve à l'extérieur du cône de lumière. La particule ne peut que se
déplacer vers le centre
4 

On suppose que
la particule tombe avec un mouvement radial, c'est à dire ,
les vitesses
,
ce sont les vitesses tangentielles.
Pour simplifier
les calculs on prendra comme variable .
Ce qui change la valeur de
,
pour les calculs qui suivre elle sera égale à
4.1 Géodésique :
La métrique
avec se simplifie en
(9.4.1)
Pour trouver la trajectoire de la particule il faut chercher l'extremum de l'intégrale
. Les équations différentielles du mouvement
sont :
(9.4.2)
La variable n'apparaissant pas explicitement dans la
fonction
il reste
et donc
,
c'est-à-dire
(9.4.3)
Comme :
et
(9.4.4)
Le signe moins est choisi pour une particule "tombant" vers le centre, le rayon r est décroissant.
Si à
l'instant initial la particule est immobile au point ,
en ce point
et
,
.
Les équations deviennent
(9.4.5)
4.2 "Temps de chute"
Ce qui permet
d'exprimer en fonction de
:
(9.4.6)
Partant
de pour atteindre
le temps sera
(9.4.7)
Cette intégrale
peut se calculer avec des fonctions élémentaires. Si on examine ce qui se passe
lorsque est proche de
,
(9.4.8)
Cette intégrale
diverge comme lorsque
.
4.3 Le temps des observateurs
L'équation (9.4.7)indique comment varie la
variable pendant la chute de la particule. Mais comment
varie le temps des observateurs ?
4.3.1 Observateur situé au loin
On suppose que
l'observateur est situé en un point tel que ,
d'près ce qui a été vu dans le chapitre "Intervalle de temps", le
temps propre de l'observateur fixe varie comme
.
En reprenant la variation
dans(9.4.6), pour l'observateur, son
temps propre varie :
.
La seule
différence avec (9.4.6)est le facteur constant .
Lorsque la particule s'pproche du rayon de Schwarzschild
le temps propre de l'observateur croit
indéfiniment, d'autant plus vite qu l'observateur est plus loin.
4.3.2 Observateur se déplaçant avec la particule.
Sont temps
propre est mesuré par .
Avec l'équation
,
soit
le temps propre du voyageur varie comme
(9.4.9)
Cette intégrale
a une limite finie lorsque .
Un calcul élémentaire (voir en annexe) donne un temps de chute observé par cette observateur :
Avec ,
rayon initial et
tel que
et donc
Si alors
Le voyageur arrive donc en un temps limité sur la sphère de Schwarzschild. Il continue son voyage à l'intérieur du "trou noir".
Si le
"voyage" continue le temps total pour atteindre le centre est
Vitesse de chute mesurée par l'observateur se déplaçant avec la particule. L'élément de longueur
et la vitesse
en utilisant (9.4.6) et en remplaçant par sa valeur
,
il vient
et
(9.4.10)
Lorsque le "voyageur" s'approche de la sphère de Schwarzschild il mesure une vitesse de déplacement qui tend vers la vitesse de la lumière.
Au contraire pour un observateur fixe, sa vitesse tend vers zéro!!!!
4.3.3 Décalage vers le rouge
Une source
lumineuse monochromatique de période située au point
.
Quelle sera sa fréquence perçue au point situé en
?
Au point situé
en la variation de la variable
correspondant au temps propre
est
Au point situé
en ,
le temps propre correspondant à cette de
sera
(9.4.11)
.
Il y a un glissement vers le rouge. Lorsque
,
pour un observateur les phénomènes physiques observés au loin semblent se
figer.
5 

Dans le cas
d'une symétrie centrale, on peut trouver une solution en négligeant la
pression. En désignant par le temps et la coordonnée radiale.
5.1 Mise en équations d'une solution générale
On cherche une solution de la forme
(9.5.1)
La quantité .
|
Le référentiel est lié à la matière.
A chaque particule de matière correspond une valeur déterminée de |
est une fonction de
.
C'est un rayon tel que la longueur de la circonférence dont le centre est
confondu avec l'origine soit
.
Pour tenir compte de la présence de la matière seule, l'équation d'Einstein de la relativité générale s'écrit
(9.5.2)
En écrivant et
,
les équations d'Einstein sont :
(9.5.3)
5.2 Solutions
La dernière
équation s'intègre par :
Et qui peut aussi être écrit :
(9.5.4)
est une fonction arbitraire telle que
.
En reportant dans la oremière équation de (9.5.3) :
(9.5.5)
Cette équation
s'intègre également en remarquant qu'en la multipliant par et que
.
,
et intégrant par rapport à
:
Cette
équation impose que lorsque ,
(9.5.6)
Ce qui permet de
calculer :
.
En se souvenant que les fonctions
sont des fonctions de
,
cette intégrale peut se transformer :
(9.5.7)
5.2.1 Cas 

L'intégrale
devient
Pour avoir il faut
Elle s'intègre
en posant et
et
en posant
(9.5.8)
La fonction est une "constante" d'intégration
arbitraire.
5.2.2 Cas 

On pose 
 .
L'équation (9.5.7) s'écrit
.
L'équation (9.5.7) s'écrit 

Elle s'intègre
en posant et
c'est-à-dire
.
En posant encore
(9.5.9)
5.2.3 Cas 

Dans ce cas
l'équation (9.5.6) se réduit à
en élevant au carré et en extrayant la racine
cubique :
(9.5.10)
5.2.4 Densité de matière
En reportant la
valeur de dans l'équation ( 3) de (9.5.3) et en utilisant
de (9.5.6)on démontre (voir en
annexe) que
(9.5.11)
5.3 Masse totale d'une sphère
L'élément de
volume entre les rayons est
Comme ,
(9.5.12)
Ce qui donne
également ,
étant le rayon de Schwarzschild de la boule de
matière de rayon
Si ,
alors
.
On se trouve dans le cas étudié par Schwarzschild, mais avec une solution
valable également à l'intérieur de la sphère de rayon
.
Le choix des
fonctions étant libre, si on choisit
,
on retrouve la métrique (9.1.10) :
Voir
démonstration en annexe. est remplacé par
et
par
.
5.4 Remarque sur les solutions
La solution
générale dépend apparemment de 3 fonctions ,
mais la coordonnée
peut être soumise à une transformation
arbitraire
.
Si on donne des
valeurs arbitraires à ces fonctions, à condition qu'elles soient comprises
entre ,
on obtient le mouvement de la sphère de ce rayon
.
Cette solution ne dépend pas des valeurs de ces fonctions pour
.
Dans tous les
cas lorsque ,
le rayon
.
La particule atteint le centre de la sphère. Si
,
toutes les particules arrivent en même temps au centre de la sphère. Toutes les
distances radiales et toutes les distances circonférentielles tendent vers
zéro.
Voir en annexe une solution donnant le référentiel permettant de décrire le champ créé par une masse ponctuelle, à l'extérieur et à l'intérieur de la sphère de Schwarzschild.
5.5 Collapse de la sphère de poussière initialement au repos
5.5.1 Mise en équation
Il s'agit de
choisir les fonctions .
La solution proposée par LANDAU est
En reportant ces valeurs dans la formule (9.5.9)
:
(9.6.1)
La densité de
matière
(9.6.2)
Avec donné par (9.6.1) et qui peut être écrit
car suivant la deuxième équation de (9.6.1) u est une fonction de la
seule variable
,
la métrique
peut s'écrire,
avec
(9.6.3)
A un instant
donné ,
c'est-à-dire pour une valeur donnée de
la densité de matière ne dépend pas de
.
La densité de matière est la même en tout point.
Les valeurs de doivent être ajustées aux conditions
initiales. A l'instant initiale, la matière de la sphère est au repos :
,
ce qui s'écrit pour une valeur de
donnée d'après (9.6.1) :
(9.6.4)
La vitesse nulle
correspond à .
L'instant où la particule atteint le centre, c'est-à-lorsque
correspond à
.
Par commodité, on remplace
par
.
Les équations (9.6.1) deviennent :
(9.6.5)
L'instant correspond
:
,
les équations (9.6.5) deviennent
(9.6.6)
A l'instant :
.
Le rayon de la
sphère de Schwarzschild est
5.5.2 Durée du collapse
La vitesse de
chute est d'après (9.6.6) .
Lorsque le rayon tend vers 0,
tend vers
et les vitesses tendent vers l'infini!!!
Le centre est
atteint lorsque ,
(9.6.7)
5.5.3 Un calcul d'application
La masse de a
sphère de rayon est d'après (9.5.12)
.
Le rayon de la sphère de Schwarzschild peut s'écrire de 2 façon :
et , suivant
.
De ces 2 expression de
,
il sort
.
En reportant dans (9.6.7) :
(9.6.8)
Cette formule
peut se transformer, par exemple en fonction de :
Si le soleil
était une boule de poussière avec et
,
le temps de collapse serait
.
Pour la Terre, km et
5.5. Un paradoxe : le collapse dans la théorie de Newton
Voir le calcul en annexe.
Le paradoxe est que la méthode de Newton donne exactement le même résultat pour le teps de collapse.
 Pour une valeur de
Pour une valeur de